boundary layer
In physics and fluid mechanics, a boundary layer is the layer of fluid in the immediate vicinity of a bounding surface where the effects of viscosity are significant. In the Earth's atmosphere, the atmospheric boundary layer is the air layer near the ground affected by diurnal heat, moisture or momentum transfer to or from the surface. On an aircraft wing the boundary layer is the part of the flow close to the wing, where viscous forces distort the surrounding non-viscous flow. SeeReynolds number.
Laminar boundary layers can be loosely classified according to their structure and the circumstances under which they are created. The thin shear layer which develops on an oscillating body is an example of a Stokes boundary layer, while theBlasius boundary layer refers to the well-known similarity solution near an attached flat plate held in an oncoming unidirectional flow. When a fluid rotates and viscous forces are balanced by the Coriolis effect (rather than convective inertia), an Ekman layer forms. In the theory of heat transfer, a thermal boundary layer occurs. A surface can have multiple types of boundary layer simultaneously.
The viscous nature of airflow reduces the local velocities on a surface and is responsible for skin friction. The layer of air over the wing's surface that is slowed down or stopped by viscosity, is the boundary layer. There are two different types of boundary layer flow: laminar and turbulent.
Laminar Boundary Layer Flow
The laminar boundary is a very smooth flow, while the turbulent boundary layer contains swirls or "eddies." The laminar flow creates less skin friction drag than the turbulent flow, but is less stable. Boundary layer flow over a wing surface begins as a smooth laminar flow. As the flow continues back from the leading edge, the laminar boundary layer increases in thickness.
Turbulent Boundary Layer Flow
At some distance back from the leading edge, the smooth laminar flow breaks down and transitions to a turbulent flow. From a drag standpoint, it is advisable to have the transition from laminar to turbulent flow as far aft on the wing as possible, or have a large amount of the wing surface within the laminar portion of the boundary layer. The low energy laminar flow, however, tends to break down more suddenly than the turbulent layer.
The deduction of the boundary layer equations was one of the most important advances in fluid dynamics (Anderson, 2005). Using an order of magnitude analysis, the well-known governing Navier–Stokes equations of viscous fluid flow can be greatly simplified within the boundary layer. Notably, the characteristic of the partial differential equations (PDE) becomes parabolic, rather than the elliptical form of the full Navier–Stokes equations. This greatly simplifies the solution of the equations. By making the boundary layer approximation, the flow is divided into an inviscid portion (which is easy to solve by a number of methods) and the boundary layer, which is governed by an easier to solve PDE. The continuity and Navier–Stokes equations for a two-dimensional steady incompressible flow in Cartesian coordinates are given by
where  and
and  are the velocity components,
are the velocity components,  is the density,
is the density,  is the pressure, and
is the pressure, and  is the kinematic viscosity of the fluid at a point.
is the kinematic viscosity of the fluid at a point.
 and
and  are the velocity components,
are the velocity components,  is the density,
is the density,  is the pressure, and
is the pressure, and  is the kinematic viscosity of the fluid at a point.
is the kinematic viscosity of the fluid at a point.
The approximation states that, for a sufficiently high Reynolds number the flow over a surface can be divided into an outer region of in-viscid flow unaffected by viscosity (the majority of the flow), and a region close to the surface where viscosity is important (the boundary layer). Let  and
and  be streamwise and transverse (wall normal) velocities respectively inside the boundary layer. Using scale analysis, it can be shown that the above equations of motion reduce within the boundary layer to become
be streamwise and transverse (wall normal) velocities respectively inside the boundary layer. Using scale analysis, it can be shown that the above equations of motion reduce within the boundary layer to become
 and
and  be streamwise and transverse (wall normal) velocities respectively inside the boundary layer. Using scale analysis, it can be shown that the above equations of motion reduce within the boundary layer to become
be streamwise and transverse (wall normal) velocities respectively inside the boundary layer. Using scale analysis, it can be shown that the above equations of motion reduce within the boundary layer to become
and if the fluid is incompressible (as liquids are under standard conditions):
The order of magnitude analysis assumes the streamwise length scale significantly larger than the transverse length scale inside the boundary layer. It follows that variations in properties in the streamwise direction are generally much lower than those in the wall normal direction. Apply this to the continuity equation shows that  , the wall normal velocity, is small compared with
, the wall normal velocity, is small compared with  the streamwise velocity.
the streamwise velocity.
 , the wall normal velocity, is small compared with
, the wall normal velocity, is small compared with  the streamwise velocity.
the streamwise velocity.
Since the static pressure  is independent of
is independent of  , then pressure at the edge of the boundary layer is the pressure throughout the boundary layer at a given streamwise position. The external pressure may be obtained through an application of Bernoulli's equation. Let
, then pressure at the edge of the boundary layer is the pressure throughout the boundary layer at a given streamwise position. The external pressure may be obtained through an application of Bernoulli's equation. Let 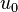 be the fluid velocity outside the boundary layer, where
be the fluid velocity outside the boundary layer, where  and
and 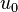 are both parallel. This gives upon substituting for
are both parallel. This gives upon substituting for  the following result
the following result
 is independent of
is independent of  , then pressure at the edge of the boundary layer is the pressure throughout the boundary layer at a given streamwise position. The external pressure may be obtained through an application of Bernoulli's equation. Let
, then pressure at the edge of the boundary layer is the pressure throughout the boundary layer at a given streamwise position. The external pressure may be obtained through an application of Bernoulli's equation. Let 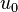 be the fluid velocity outside the boundary layer, where
be the fluid velocity outside the boundary layer, where  and
and 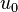 are both parallel. This gives upon substituting for
are both parallel. This gives upon substituting for  the following result
the following result
For a flow in which the static pressure  also does not change in the direction of the flow then
also does not change in the direction of the flow then
 also does not change in the direction of the flow then
also does not change in the direction of the flow then
so 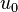 remains constant.
remains constant.
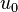 remains constant.
remains constant.
Therefore, the equation of motion simplifies to become
These approximations are used in a variety of practical flow problems of scientific and engineering interest. The above analysis is for any instantaneous laminar or turbulentboundary layer, but is used mainly in laminar flow studies since the mean flow is also the instantaneous flow because there are no velocity fluctuations present. This simplified equations is parabolic PDE and can be solved using a similarity solution often referred to as the Blasius boundary layer









No comments:
Post a Comment