Euler's theory
This article is about Euler's theorem in number theory. For other uses, see List of topics named after Leonhard Euler.
In number theory, Euler's theorem (also known as the Fermat–Euler theorem or Euler's totient theorem) states that if n and a are coprime positive integers, then
where φ(n) is Euler's totient function. (The notation is explained in the article modular arithmetic.) In 1736, Leonhard Euler published his proof of Fermat's little theorem, whichFermat had presented without proof. Subsequently, Euler presented other proofs of the theorem, culminating with "Euler's theorem" in his paper of 1763, in which he attempted to find the smallest exponent for which Fermat's little theorem was always true.[2]
The converse of Euler's theorem is also true: if the above congruence is true, then a and n must be coprime.
The theorem is a generalization of Fermat's little theorem, and is further generalized by Carmichael's theorem.
The theorem may be used to easily reduce large powers modulo n. For example, consider finding the ones place decimal digit of 7222, i.e. 7222 (mod 10). Note that 7 and 10 are coprime, and φ(10) = 4. So Euler's theorem yields 74 ≡ 1 (mod 10), and we get 7222 ≡ 74 × 55 + 2 ≡ (74)55 × 72 ≡ 155 × 72 ≡ 49 ≡ 9 (mod 10).
Note that if 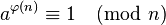 , then also
, then also  for any positive k, because of
for any positive k, because of
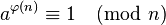 , then also
, then also  for any positive k, because of
for any positive k, because of and so on.
and so on.
In general, when reducing a power of a modulo n (where a and n are coprime), one needs to work modulo φ(n) in the exponent of a:
- if x ≡ y (mod φ(n)), then ax ≡ ay (mod n).
Euler's theorem also forms the basis of the RSA encryption system, where the net result of first encrypting a plaintext message, then later decrypting it, amounts to exponentiating a large input number by kφ(n) + 1, for some positive integer k. Euler's theorem then guarantees that the decrypted output number is equal to the original input number, giving back the plaintext.


No comments:
Post a Comment