Entropy
is a property of thermodynamic systems. The term entropy was introduced by Rudolf Clausius who named it from the Greek word τρoπή, "transformation". He considered transfers of energy as heat and work between bodies of matter, taking temperature into account. Bodies of radiation are also covered by the same kind of reasoning.
More recently, it has been recognized that the quantity 'entropy' can be derived by considering the actually possible thermodynamic processes simply from the point of view of their irreversibility, not relying on temperature for the reasoning.
Ludwig Boltzmann explained the entropy as a measure of the number of possible microscopic configurations Ω of the individual atoms and molecules of the system (microstates) which comply with the macroscopic state (macrostate) of the system. Boltzmann then went on to show that k ln Ω was equal to the thermodynamic entropy. The factor k has since been known as Boltzmann's constant
According to the Clausius equality, for a closed homogeneous system, in which only reversible processes take place,
With T being the uniform temperature of the closed system and delta Q the incremental reversible transfer of heat energy into that system.
That means the line integral 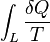 is path independent.
is path independent.
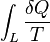 is path independent.
is path independent.
So we can define a state function S, called entropy, which satisfies



No comments:
Post a Comment